Logic
Rhyming Notes on Philosophy #05
Language in deadlock, died in her swan song,
arguments lost all power in words,
How can we validate our artisanal science,
prove our philosophy to scientific nerds?1
No greyness, no middle, no plausible story,
philosophical discourse compressed and condensed,
So let's state our ideas as premises, predicates,
by new connectives, results will be fenced.
Join my trip to an alternative universe,
where language and sentences are shortened to runes,
truth calculated and inconsistency cursed,
with tautological certainty, discussion is pruned.
In this Logical Land, they've abbreviated language,
converging conversing, poetic erosion,
essence abstracting, simplicity reigns:
P and not-P then Q - in a deductive explosion2.
All truth can be proven on a semantic tableau,
closing branches do prove it, because you will see,
Here truth is proved if, in no conceivable way,
You can make its negation to be3.
Evidence relies on believe in itself,
intuitive translation to language can't be done:
if we still fail to convince someone outside this world,
that something ís, because of the zero is one.
Symbolic concluding postscript
I propose after this poetic delation,
that logic is philosophy's ᆨ
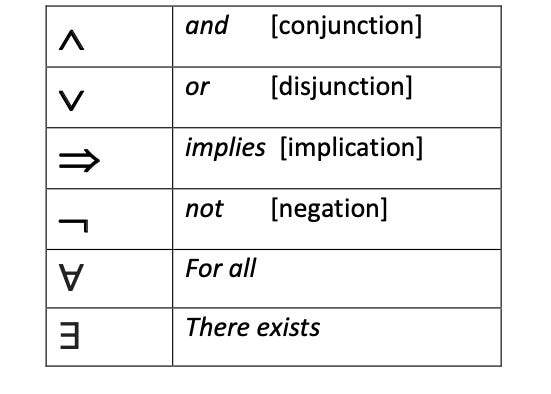
and in ⋀ with wordless analytics
their → is limited metaphysics.ᆨ : negation
⋀ : conjunction
→: implication
A second tool for the philosopher is the wonderful world of logic. In search of a verdict between true and false, logic is the debater's language. Perhaps you know the most classic syllogism:
(Premise 1) All humans are mortal
(Premise 2) Socrates is a human being
(Conclusion) Socrates is mortal
But that is just where it starts. Text can be shortened to letters that express the relationship between arguments. And then via a miracle formula follows a “0” or a “1”.
Logic, as the study of valid reasoning, has been part of philosophy since its start. However, contesting the natural sciences, a certain want to become a “matured” science revitalized the study of logic as part of epistemology. Learn more: Logic in Action.
The deductive explosion refers to the principle that as soon as a contradiction is asserted, any proposition can be inferred from it. So; if a contradiction is logical valid; then anything goes! Of course, if it holds, it only has any consequences if there ever is a contradiction that is logical valid. So a situation in which P is true ánd its negation ᆨP is true.
(p1) P = true
(p2) ᆨP = true
(p3) P∨Q = true : (p1 is true. So, the disjunction of P and any Q is valid. Even if Q means that the moon is made of cheese)
(c) Q = true : (The combination of p3 and p2 leads to the conclusion that Q is true - so the moon is made of cheese!)
But: is there a situation in which a proposition P and its negation are both true? Well, as Russell pointed out there is such a situation, Russell’s paradox. More on that later.
The tableau system is a method to validate logical statements. By constructing the consequences of counter-examples and concluding that none of these are valid, the logical inference is valid. See: Method of analytic tableaux.